理解贝叶斯定理的两种思路

2017-03-14 23:03 数学·AI 数学 , 贝叶斯

理解贝叶斯定理的两种思路

贝叶斯定理

本文将通过一个例子，介绍如何用贝叶斯定理来求得后验概率，并且给出了两种解题的方式。所以，贝叶斯公式具体如何推导而来，这里不再赘述，我们直接贴出贝叶斯定理公式：

p(A | B) = \frac{p(A)p(B|A))}{p(B)}

假设 ${A{j}}$ 是事件集合里的部分集合，对于任意的 ${A{i}}$ ，引入全概率公式后，贝叶斯定理变为：

p(A{i}| B) = \frac{p(A{i})p(B|A{i})}{\sum_{j}p(A{j})p(B|A{j})}

其中p(A)称为先验概率， p(A|B)称为后验概率。

范例：吸毒者检测

问题来自维基百科，描述如下：

假设一个常规的检测结果的敏感度与可靠度均为99%，即吸毒者每次检测呈阳性（+）的概率为99%。而不吸毒者每次检测呈阴性（-）的概率为99%。假设某公司对全体雇员进行吸毒检测，已知0.5%的雇员吸毒。请问每位检测结果呈阳性的雇员吸毒的概率有多高？

思路一：套公式

令“D”为雇员吸毒事件，“N”为雇员不吸毒事件，“+”为检测呈阳性事件。

将公式带入后，得到答案是0.3322。

\begin{aligned}P(D|+)&={\frac {P(+|D)P(D)}{P(+)}}\\&={\frac {P(+|D)P(D)}{P(+|D)P(D)+P(+|N)P(N)}}\\&={\frac {0.99\times 0.005}{0.99\times 0.005+0.01\times 0.995}}\\&=0.3322.\end{aligned}

但是，这种方式是”没感情“，”不自然“的，至少本人是这么觉得。🤣

思路二：历时诠释

历时诠释（The diachronic interpretation），是另一种理解贝叶斯定理的思路：他给我们提供的是一种根据数据集D到内容变化更新假设概率H 的方法。有些文章把D也称为证据，并表示为E，两者是同一个东西

此时的贝叶斯定理变为：

p(H | D) = \frac{p(H)p(D|H))}{p(D)}

p(H) 称为先验概率，在D没发生之前某一假设的概率。
p(H|D)称为后验概率，也是我们要求得的概率。
p(D|H)为在该假设下得到这一数据的概率，称为似然度。
p(D)是在任何假设下得到这一数据的概率，称为标准化常量。

所以，贝叶斯定理也等价于：

后验概率 = \frac{相似度*先验概率}{标准化常量}

我们来用历时诠释的角度来解吸毒者检测这道题，首先我们枚举所有假设：

H1：吸毒者
H2：未吸毒者

很显然，这里D表示为检测呈阳性，然后用表格列出每一项：

	先验概率p(H)	似然度p(D\|H)	p(H)p(D\|H)	后验概率p(H\|D)
H1	0.5	99	49.5	0.3322
H2	99.5	1	99.5	0.6678

由此我们已经得到了H1的答案0.3322。

其中第四列中的和(49.5+99.5=149)，我们叫归一化常数，后验概率通过49.5 / 149=0.3322求得。正如我们所看到的，归一化常数和标准化常量可能值不同，但它们是代表的同一个含义。如果表中的数值是严格的概率，比如似然度是0.99，而不是99，那求出来的归一化常数就等于标准化常量。但实际上，这个数值放大100倍或者1000倍都不影响计算结果，因为在除以归一化常数时抵消掉了。

思路二解题方式的一个变种

在知乎上，发现某大神用用先验概率比、似然比、后验概率比的方式，来计算概率。其实跟上面的方式本质上是一样，但方式上有点新颖。此知乎问题的地址是：怎样用非数学语言讲解贝叶斯定理，下面我贴出此知乎问题和回答。

以下内容为转载

问题

昨天看到这样一道题，感觉是可以用简单的逻辑推论出来的。但是总是差一点点。一机器在良好状态生产合格产品几率是 90%，在故障状态生产合格产品几率是 30%，机器良好的概率是 75%。若一日第一件产品是合格品，那么此日机器良好的概率是多少。

求逻辑推论，我知道拿公式来解速度很快，但这终究是速成法，不能内化。这种逻辑上推导才是数学精神和乐趣所在，数学语言是人思维活动的一种表现形式，有达人能告诉我这种情况的思考方式吗？

回答（作者：伯雷）

这道题心算即可——

（1）先验比率是75% : (1-75%) = 3 : 1；

（2）似然比率（Likelihood ratio）= 90% : 30% = 3；

（3）两者相乘，得后验比率 = 9 : 1；然后

（4）标准化（normalize），得后验概率 = 9 / (9+1) = 90%。

【故事】

让我们先来做一道小学数学题。

问：假设如来佛和玉皇大帝要打架，如来拥有全宇宙战斗力的 75%，剩下的战斗力都归玉帝。那么，玉帝的战斗力占全宇宙的多少？

答：太简单了，100% - 75% = 25%

问：此时，如来和玉帝的战力比是多少？

答：容易，75% : 25% = 3 : 1。

问：好了，现在，假设太上老君发明了一种仙丹，能增强战斗力，如来佛和玉帝都偷吃了一颗。可是，如来和玉帝体质不同——如来吃了之后，战斗力增加了 90 倍；玉帝吃了之后，战斗力只增加 30 倍。请问，两人偷吃仙丹之后，如来佛和玉帝的战力比变成了多少？

答：这也不难——如来相对战斗力 = 3 x 90 = 270，玉帝相对战斗力 = 1 x 30 = 30。因此，如来战力：玉帝战力 = 270 : 30 = 9 : 1

问：好了，如来、玉帝吃了仙丹之后，如来占全宇宙战斗力的多大比例？

答：如来战斗力占比 = 9 / (9 + 1) = 90%。

【解释】

我觉得，理解贝叶斯定理的最大障碍，不是原理，而是太多小数、分数、百分数，比来比去、极易混淆。如果全部都是整数，那就好理解多了。实现方法是，先把题目的小数化为整数（之比），作运算，最后再化为小数。

现在让我把上面的故事翻译一下，套到题目上。

(1) 你一开始有两个假说，良好（H1）和故障（H2）， H1和H2的先验概率比 = P(H1) : P(H2) = 3 : 1。【用P(良好) = 75%即可推出。】

(2)现在你拿到了一个证据E：第一天产品是合格的。这个证据的作用，在于改变两个假说的概率之比。

根据贝叶斯定理，这个「1 个零件合格」的证据会产生两个效果：

a. 会让「机器良好」(H1) 的相对概率增加 90 倍【因为 P(E|H1) = 90% 】，及

b. 会让「机器故障」(H2) 的相对概率增加 30 倍【因为 P(E|H2) = 30% 】。【公式上看，应该是分别缩减到 0.9 倍和 0.3 倍，但是化为整数比较容易思考。】

(3) 根据(2)，我们有了证据 E 之后，良好和故障的概率之比变为 3 x 90 : 1 x 30 = 270 : 30 = 9 : 1。

这就是一开始的计算思路。

【公式】

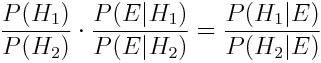
对应刚才的推理的，是贝叶斯定理常见形式的一个变体——分别对H1、H2列式，两式相除即可得。

最左边一项是先验比率（如来和玉帝吃仙丹前的实力对比），

中间一项是似然比率（仙丹对两人的效用比），

最右边一项是后验比率（如来和玉帝吃了仙丹后的实力对比）。

上述运算过程，实际上用的是下式，与上式有微妙区别：

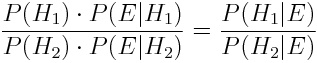
【拓展】

这个形式的好处是非常容易拓展，比如说，如果要考虑3个（独立的）证据Ea、Eb、Ec：

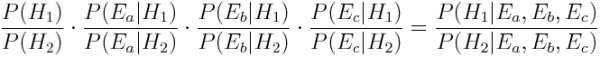
回到原题。若问，假设这个机器第一天不是生产了 1 个零件，而是生产了 3 个零件，而且 3 个都合格（零件合格的概率互相独立），那机器良好的概率是多少？

（用故事的语言就是，如果如来和玉帝连吞3颗仙丹，那么如来的战斗力占全宇宙的多少？）

答案：

P(良好|3个合格) : P(故障|3个合格) = (3 : 1) x 3 x 3 x 3 = 81 : 1。【3 个合格零件，所以乘3次】

假设 P(良好|3个合格) + P(故障|3个合格) = 1，则

P(良好|三个合格) = 81 / (81 + 1) = 98.8%

参考

书籍《贝叶斯思维》
知乎怎样用非数学语言讲解贝叶斯定理